دالة الإنتاج Production Function هي معادلة رياضية تحدد العلاقة بين عوامل وكمية المدخلات للإنتاج وعدد السلع التي تنتجها بأكبر قدر من الكفاءة. ودالة الإنتاج تجيب على الاستفسارات المتعلقة بالناتج الحدي ومستوى الإنتاج وأرخص طريقة لإنتاج السلع.
ما هو علم الاقتصاد؟
علم الاقتصاد هو العلم الذي يدرس القواعد المنظمة للسلوك الاقتصادي من خلال استخدام الوسائل المادية و الموارد المحدودة لإشباع الحاجات الإنسانية المتعددة. وعلي ذلك فالمشكلة الاقتصادية تتمثل في كيفية إشباع الحاجات المتزايدة باستخدام الموارد المحدودة.
مقالة ذات صلة: علم الاقتصاد: تعريفه، أهميته، فروعه، مناهجه
دالة الانتاج
تختص نظرية الانتاج بدراسة علاقة كميات عناصر الإنتاج المستخدمة في العملية الانتاجية، وكمية الناتج الكلي المتحقق من هذه العملية، وهذه العلاقة تسمى “دالة الانتاج”. وإذا عبرنا عن هذه العلاقة في شكل معادلة رياضية فإننا نكتبها كالتالي:
ن ك = د (ل، ض، ر، ت).
حيث؛
ن ك: الناتج المحلي.
ل: عنصر العمل.
ض: عنصر الأرض.
ر: عنصر رأس المال.
ت: عنصر التنظيم
أي أن الناتج الكلي هو دالة في (أي يعتمد على) المدخلات من عناصر الانتاج المتمثلة في العمل والأرض ورأس المال والتنظيم، حيث الناتج الكلي متغير تابع، وعناصر الانتاج متغيرات مستقلة، بمعني أن حجم الناتج الكلي يتوقف على الكميات المستخدمة من هذه العناصر الانتاجية. ذلك أن انتاج أي سلعة من السلع لابد وأن يتطلب تضافر أكثر من عنصر واحد من عناصر الإنتاج. فنجد مثلاً أن العمل وحدة لا يمكن أن ينتج سلعة ما، بل يتطلب الأمر الاستعانة بمقدار معين من رأس المال، حتى ولو كان على شكل بعض المعدات البسيطة التي يستخدمها العامل. كذلك نجد أن رأس المال لا يمكن وحدة أن يقوم بالإنتاج مهما بلغت العملية الانتاجية من درجة عالية من الآلية، إذ أن الأمر لابد وأن يستلزم قدراً معيناً من العمل، سواء لإدارة الآلات أو الأشراف عليها.
فإذا نظرنا إلى عملية الانتاج الزراعي، نحد أن هذه العملية تحتاج إلى تضافر أكثر من عنصر واحد من عناصر الإنتاج. فلا يمكن الاعتماد على عنصر الأرض وحده، بل لابد على الأقل من تضافر عنصر العمل والأرض. فإذا أردنا زراعة فدان قمح، فلا يمكن زراعة هذا الفدان بدون وجود عمال زراعيين. وقد يحتاج الأمر وجود بعض المعدات أو الأدوات الزراعية البسيطة وهكذا، فإن زراعة هذا الفدان تتطلب تضافر عناصر الأرض والعمل ورأس المال. ونشير إلى أنه يمكن الحصول على نفس حجم الإنتاج باستخدام نسب مزج مختلفة من عناصر الإنتاج، حيث يمكن في مثالنا السابق استخدام فن انتاجي كثيف العمل، أي بالاعتماد على عدد كبير من العمال الزراعيين مع الاستعانة ببعض المعدات الرأسمالية البسيطة، أو بالاعتماد على عدد قليل من العمال الزراعيين، مع الاعتماد الرئيسي على الميكنة الزراعية (فن انتاجي كثيف رأس المال).
الافتراضات عند دراسة دالة الإنتاج
وعند دراستنا لدالة الإنتاج سنفترض ما يلي:
1. نفترض أن العملية الانتاجية تتم في خلال فترة معينة من الزمن
نفترض أن العملية الانتاجية تتم في خلال فترة معينة من الزمن، ومن ثم فإن كمية الناتج الكلي هي كمية متحققة خلال فترة معينة من الزمن، وعليه حينما نتكلم عن تغير الناتج بالزيادة أو بالنقص فإننا نقصد أن يتم هذا التغير في خلال نفس الفترة من الزمن وليس في فترة أطول أو أقصر.
2. نفترض أن عناصر الانتاج متجانسة
نفترض أن عناصر الانتاج متجانسة (العمل والأرض ورأس المال)، أي أن وحداتها متماثلة تمام التماثل، وأن بالإمكان قياس الكمية المستخدمة من كل عنصر منها قياساً عددياً. وبالنسبة لعنصر التنظيم فإننا نسقطه صراحة من معادلة دالة الانتاج في الفترة لذا نكتب المعادلة كالآتي: ن ك = (ل، ض، ر)، بافتراض مستوي معين من المقدرة التنظيمية لا يتغير خلال فترة العملية الانتاجية.
أما بالنسبة لمعادلة دالة الانتاج في الفترة طويلة الأجل، فأننا لا نستطيع التخلي عن ذكر عنصر التنظيم صراحة. والفرق بين ظروف دالة الانتاج في الفترة القصيرة الأجل والفترة الطويلة الأجل هو الذي يجعلنا نتبع هذا الحل. ففي خلال الفترة القصيرة الأجل تتغير الكمية المستخدمة من العناصر المتغيرة فقط. بينما تبقي الكمية المستخدمة من العناصر الانتاجية الثابتة كما هي، ولذلك يمكننا أن نفترض أن عنصر التنظيم يدخل ضمن العناصر الثابتة ونخرجه من معادلة دالة الانتاج صراحة مع استبداله بفرض مستوي معين ثابت من المقدرة التنظيمية.
أما في الفترة الطويلة الأجل فأن جميع العناصر تتغير بما فيها عنصر التنظيم، و لذلك لا بد من ظهوره في معادلة دالة الانتاج مع بقية العناصر الأخرى. وتجاوزاً لا بد من افتراض إمكانية قياسه في هذه الحالة، مع ملاحظة أن النوع أهم بكثير من العدد بالنسبة لعنصر التنظيم فمدير واحد مثلاً قد يستطيع انجاز أعمال تساوي ما يمكن لخدمة آخرون أن ينجزوه معاً.
3. نفترض أن مستوى الفن التكنولوجي ثابت غير متغير
ج. نفترض أن مستوي الفن التكنولوجي ثابت غير متغير خلال الفترة الزمنية المعينة لعملية الانتاج. ذلك أن تحسن مستوي الفن التكنولوجي يؤدي دائماً إلى زيادة انتاجية العناصر المستخدمة، ومن ثم زيادة الناتج الكلي مع ثبات الكميات المستخدمة من عناصر الانتاج في العملية الانتاجية. وعليه نفترض ثبات مستوي الفن التكنولوجي حتى يكون أي تغير في الناتج الكلي راجع إلى تغير الكميات المستخدمة من عناصر الانتاج.
أهمية دالة الإنتاج
تعد دالة الإنتاج مفهومًا مهمًا في الاقتصاد يوضح العلاقة بين المدخلات (مثل العمالة ورأس المال والتكنولوجيا) والمخرجات (السلع أو الخدمات) في عملية الإنتاج. فيما يلي بعض الأسباب التي تجعل دالة الإنتاج مهمة:
- فهم عمليات الإنتاج: توفر دالة الإنتاج إطارًا لفهم كيفية دمج المدخلات وتحويلها إلى مخرجات في عملية الإنتاج. وتساعد الاقتصاديين والشركات على تحليل العوامل التي تساهم في الإنتاج وتحديد أكثر الطرق فعالية لتنظيم الإنتاج.
- تخصيص الموارد: توجه دالة الإنتاج القرارات المتعلقة بتخصيص الموارد النادرة في عملية الإنتاج. فمن خلال تحليل العلاقة بين المدخلات والمخرجات، يمكن للشركات تحديد التركيبة المثلى للمدخلات التي تؤدي إلى أعلى ناتج ممكن في ظل قيود الموارد. وتساعد هذه المعلومات في اتخاذ قرارات مستنيرة حول تخصيص الموارد، مثل تحديد المستويات المثلى للعمل ورأس المال والتكنولوجيا لاستخدامها.
- تحليل الكفاءة: يتم استخدام دالة الإنتاج لتقييم كفاءة عمليات الإنتاج. فدالة الإنتاج تسمح للشركات بمقارنة مستويات الإنتاج الفعلية بمستويات الإنتاج المحتملة في ظل مجموعات مختلفة من المدخلات. ومن خلال فحص العلاقة بين المدخلات والمخرجات، يمكن تحديد أوجه القصور في عملية الإنتاج واستهدافها للتحسين.
- تخطيط الإنتاج والتنبؤ به: تعتبر دالة الإنتاج مفيدة في تخطيط الإنتاج والتنبؤ به. ومن خلال فهم العلاقة بين المدخلات والمخرجات، يمكن للشركات تقدير كمية المدخلات المطلوبة لإنتاج المستوى المطلوب من المخرجات. وتساعد هذه المعلومات في تحديد أهداف الإنتاج وتحديد متطلبات الموارد والتخطيط لاحتياجات الإنتاج المستقبلية.
- تحليل التكلفة: ترتبط دالة الإنتاج ارتباطًا وثيقًا بتحليل التكلفة. وتساعد دالة الإنتاج الشركات على فهم العلاقة بين المدخلات والمخرجات والتكاليف. ومن خلال تحليل دالة الإنتاج، يمكن للشركات تحديد كيفية تأثير التغييرات في أسعار المدخلات أو التكنولوجيا على التكاليف. وهذه المعلومات ذات قيمة لقرارات التسعير ومراقبة التكاليف وتحسين الأرباح.
مقالة ذات صلة: تكاليف الإنتاج في الاقتصاد الجزئي: ما هي، أنواعها، أمثلة عليها
أنواع دالة الإنتاج
هناك نوعان رئيسيان من دالة الإنتاج، وهما دالة الإنتاج في الفترة قصيرة الأجل و دالة الإنتاج في الفترة طويلة الأجل، ، كما هو موضح أدناه:-
1. دالة الإنتاج في الفترة قصيرة الأجل
الفترة القصيرة — كما سبق وذكرنا هي التي تتغير فيها عناصر الانتاج المتغيرة فقط في حين تبقي عناصر الانتاج الثابتة على حالها. وتوضح دالة الانتاج في الفترة القصيرة كيف يتغير حجم الانتاج إذا تغيرت الكمية المستخدمة من عناصر الانتاج المتغيرة فقط. وسنفترض وجود دالة انتاج مبسطة ومكونه من عنصرين انتاجيين فقط أحدهما متغير وهو العمل، والآخر ثابت وهو الأرض. وسنفترض كمية ثابتة من الأرض ولتكن فدان واحد، ونبدأ بإضافة وحدات متتالية من العمل لإنتاج سلعة معينة، ولتكن القمح. ومع إضافة وحدات متتالية من العمل، يأخذ الناتج الكلي في التزايد كما في الجدول التالي:
| الأرض | وحدات العمل | الناتج الكلي | الناتج المتوسط | الناتج الحدى | المرحلة |
| 1 | 1 | 2 | 2 | 2 | المرحلة الأولي |
| 1 | 2 | 6 | 3 | 4 | |
| 1 | 3 | 14 | 4.667 | 8 | |
| 1 | 4 | 20 | 5 | 6 | المرحلة الثانية |
| 1 | 5 | 25 | 5 | 5 | |
| 1 | 6 | 28 | 4.667 | 3 | |
| 1 | 7 | 28 | 4 | صفر | |
| 1 | 8 | 24 | 3 | 4- | المرحلة الثالثة |
| 1 | 9 | 18 | 2 | 6- |
يوضح الجدول السابق أن تشغيل عامل واحد على مساحة فدان من الأرض سيكون النتيجة هي انتاج (2) أردب من القمح. ومع زيادة وحدات العمل إلى عاملين، يصبح الناتج الكلي (6) أردب من القمح، أي أكثر من ضعف انتاجية العامل الأول، مما يشير إلى زيادة انتاجية عنصر العمل بعد إضافة العامل الثاني، حيث يؤدي إضافة هذا العامل إلى الاستفادة من مزايا التخصص وتقسيم العمل. ومع إضافة العامل الثالث يصبح الناتج (14) أردب من القمح، أي أن العامل الثالث أضاف (8) أرادب من القمح، في حين أضاف العامل الثاني (4) أردب من القمح ويعني ذلك أن تشغيل العامل الثالث أدي إلى زيادة الاستفادة من التخصص وتقسيم العمل.
وهكذا، تؤدي زيادة العمال بوحدات متتالية إلى زيادة متزايدة في الناتج الكلي، أي زيادة الناتج الكلي بمعدل متزايد. و لكن إلى حد معين، بعدها يزيد الناتج بمعدل متناقص ثم يصل الناتج لأقصاه ويثبت، ثم يأخذ في التناقص، حيث تكون فرص التخصص وتقسيم العمل قد استنفذت.
ويلاحظ أن الجدول السابق يتضمن ثلاثة متغيرات وهي:
- الناتج الكلي: ويقصد به الكمية الكلية المنتجة من السلعة خلال فترة العملية الإنتاجية.
- الناتج المتوسط: وهو يمثل نصيب العامل الواحد من الإنتاج في المتوسط. حيث: الناتج المتوسط = الناتج الكلي / عدد العمال
- الناتج الحدي: ويمثل الزيادة في الإنتاج الكلي نتيجة إلى زيادة وحدات العمل بوحدة واحدة. أي هو ناتج العامل الأخير. حيث: الناتج الحدي= التغير في الناتج الكلي / التغير في وحدات العنصر المتغير
وقد يكون من المهم أن نقوم هنا بدراسة خصائص كل من هذه المتغيرات أو دراسة العلاقات التي تربط بينها.
أ. العلاقة بين الناتج الكلي والناتج الحدي
من الجدول السابق، يتضح أن الناتج الكلي يمر بثلاثة مراحل:
المرحلة الأولى: يتزايد فيها الناتج الكلي بمعدل متزايد، مع إضافة وحدات متتالية من عنصر العمل، وتنتهي هذه المرحلة مع إضافة العامل الثالث. فالعامل الثالث يضيف إلى الناتج الكلي مقداراً أكبر مما يضيفه العامل الثاني الذي يضيف بدوره إلى الناتج الكلي مقداراً أكبر مما يضيفه العامل الأول. ويصاحب هذه المرحلة تزايد في الناتج الحدي وهذا منطقي، حيث أن الناتج الحدي هو ناتج العامل الأخير. ولما كان الناتج الذي يضيفه كل عامل في هذه المرحلة أكبر من ناتج العامل الذي يسبقه. فمعني ذلك زيادة الناتج الحدي.
المرطة الثانية: يزيد فيها الناتج الكلي، ولكن بمعدل متناقص وتبدأ هذه المرحلة مع إضافة العامل الرابع. حيث ترتب على إضافة هذا العامل زيادة الناتج الكلي من (14) أردب إلى (20) أردب من القمح. أي زيادة الناتج الكلي بمقدار 6 أردب فقط (مقارنة ب 8 أردب هي كمية الزيادة في الناتج الكلي المترتب على تشغيل العامل الثالث). وتستمر الزيادة في الناتج الكلي في التناقص مع زيادة عنصر العمل بوحدات متتالية، ويبلغ الناتج الكلي أقصاه عند تشغيل العامل السادس (28 أردب)، ومع تشغيل العامل السابع يثبت الناتج الكلي عند مستوي (28 أردب)، مما يشير إلى أن العامل السابع لم يضف شيئاً للإنتاج.
ويصاحب هذه المرحلة تناقص الناتج الحدي. طالما الناتج الكلي يزيد بمعدل متناقص، فمعني ذلك أن الناتج الحدي، وهو الزيادة في الناتج الكلي نتيجة إضافة عامل واحد، ولا بد وأن يكون متناقص. وحينما يصل الناتج الكلي لأقصاه، ويثبت عند هذا المستوي (عند تشغيل العامل السابع)، يكون الناتج الحدي مساوياً للصفر، حيث أن تشغيل هذا العامل لم يضف شيئاً للإنتاج.
المرطة الثالثة: وتبدأ هذه المرحلة مع إضافة العامل الثامن وفيها يتناقص الناتج الكلي، ويصبح الناتج الحدي سالباً. حيث يترتب على تشغيل عامل إضافي انخفاض حجم الانتاج وبالتالي تكون انتاجية هذا العامل سالبة. وعادة ما تستبعد المرحلة الثالثة عند دراستنا للاقتصاد، لأننا عادة نفترض في أي منتج من المنتجين صفة الرشد الاقتصادي، بمعني أن المنتج لن يضيف عامل جديد وهو يعلم أن إضافة هذا العامل يترتب عليها خسارة. والناتج الحدي بيانياً، كما في الشكل التالي:
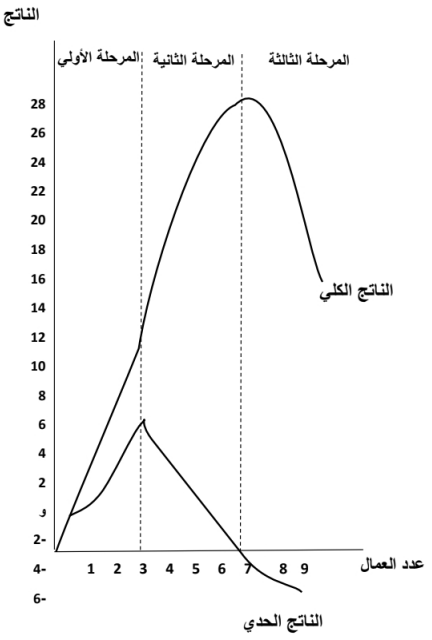
في الشكل السابق، نقيس الإنتاج على المحور الرأسي، وعدد العمال على المحور الأفقي، ونلاحظ في هذا الشكل ما يلي:
- أن الناتج الحدي يكون متزايد حتى إضافة العامل الثالث، مما يشير إلى أن الناتج الكلي يزيد بمعدل متزايد.
- عند إضافة العامل الثالث، يصل الناتج الحدي إلى أعلى قيمة له، وبعدها يأخذ في التناقص حتى إضافة العامل السادس، مما يشير إلى أن الناتج الكلي يزيد بمعدل متناقص.
- عند إضافة العامل السابع، يصبح الناتج الحدي مساويا للصفر، وهنا يصل الناتج الكلي إلى أعلى قيمة له.
- بعد إضافة العامل السابع، يصبح الناتج الحدي سالبا، وهذا معناه تناقص الناتج الكلي.
ب. العلاقة بين الناتج الحدي والناتج المتوسط
نلاحظ أن هناك علاقة بين مراحل التغير في الناتج المتوسط، وبين مراحل التغير في الناتج الحدي، وذلك على النحو التالي:
- حينما يكون الناتج المتوسط متزايد، يكون الناتج الحدي أكبر منه,
- حينما يبدأ الناتج الحدي في التناقص يستمر الناتج المتوسط في التزايد ما دام الناتج الحدي أعلى منه.
- حينما يصل الناتج المتوسط لأقصاه، يتساوى مع الناتج الحدي. (ويتحقق ذلك عند إضافة العامل الخامس).
- حينما يتناقص الناتج المتوسط، يكون الناتج الحدي أقل منه. والشكل التالي يبين العلاقة بين هذين المتغيرين:-
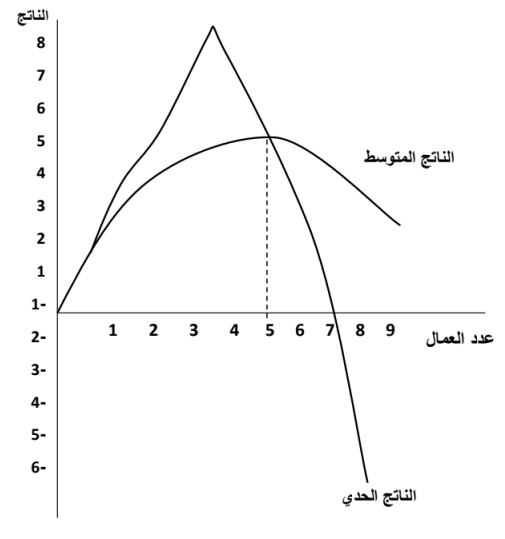
ويلاحظ من الشكل السابق ما يلي:
- أن منحنى الناتج الحدي يكون أعلى من منحنى الناتج المتوسط في مرحلة تزايد الأخير.
- أن منحنى الناتج الحدي يكون أقل من الناتج المتوسط ما دام الأخير متناقصاً.
- منحنى الناتج الحدي يبدأ في التناقص قبل منحنى الناتج المتوسط
- يقطع منحنى الناتج الحدي منحنى الناتج المتوسط عند أعلى نقطة أعلى نقطة له، مما يشير إلى تساوي الناتج الحدي مع الناتج المتوسط حينما يصل الأخير إلى أقصاه (ويتحقق ذلك عند إضافة العامل الخامس).
قانون تناقص الغلة
رأينا فيما سبق المراحل التي يمر بها كل من الناتج الحدي أو الكلي أو المتوسط ما بين زيادة في البداية تم نقص في النهاية، وذلك مع استمرار إضافة وحدات متتالية من عنصر الإنتاج المتغير إلى عنصر الانتاج الثابت. ولقد كان مصطلح “قانون تناقص الغلة” هو المصطلح الذي اتخذ لوصف هذه الظاهرة.
وينص قانون تناقص الغلة على أن إضافة وحدات متتالية من أحد عناصر الإنتاج إلى كمية ثابتة من عنصر آخر، يؤدي بعد حد معين إلى تزايد الناتج الكلي بمعدل متناقص، أي تناقص الناتج الحدي.
وواضح من صياغة هذا القانون أنه يركز أساساً على إحدى مراحل الإنتاج الثلاثة السابق الإشارة إليها ولقد كان الاقتصاديون الكلاسيك هم أول من اكتشف ظاهرة تناقص الغلة. ورأي هؤلاء الاقتصاديون أن قانون تناقص الغلة لا ينطبق إلا في مجال النشاط الزراعي فقط. وكان اعتقادهم هذا مؤسساً على مشاهدتهم الواقعية. ففي مجال الزراعة لاحظوا أن عنصر الأرض الزراعية ثابت كما ونوعاً، وأن مستوى المعرفة الفنية يكاد يكون ثابتاً لا يتغير، بينما أن عدد العمال الزراعيين في تزايد مستمر. ولكن مع تقدم التحليل الاقتصادي ثبت أن حالة تناقص الغلة يمكن أن تتحقق في أي نشاط من الأنشطة الاقتصادية زراعي أو صناعي او خدمات، طالما تحققت الظروف المهيئة لحدوثها، وهي ظروف دالة النسب المتغيرة.
والمقصود بها تغير النسب التي يتم بها مزج عناصر الإنتاج عن طريق تثبيت بعض العناصر وزيادة أحدها. فإذا ظل عدد العمال المستخدمون في أحد المصانع يتزايد مع ثبات كمية رأس المال عن الآلات والمباني والتجهيزات، ومع ثبات مستوى المعرفة الفنية والتنظيمية، فإن الناتج الكلي سوف يزيد أولاً، ولكن نهائياً لا بد أن يتناقص
والوسيلة الوحيدة لمجابهة تناقص الغلة المتوسطة عن زيادة عنصر الانتاج الثابت (وهو الأرض في مثالنا). كي تعود العلاقة بين كمية العنصر المتغير وكمية العنصر الثابت إلى النسبة إلى تتفق مع تحقيق الحد الأقصى للناتج يساوي (5) أردب قمح، ويتحقق عندما تكون نسبة العمال إلى الأرض (4: 1) على التوالي. وأن زيادة العمال بعد ذلك تؤدي إلى ثبات الناتج المتوسط ثم انخفاضه. وعندما وصل عدد العمال إلى 8 عمال، كان الناتج المتوسط يساوي (3) أردب قمح.
والوسيلة الوحيدة في هذه الحالة لضمان عدم انخفاض الانتاجية المتوسطة من أعلى مستوى وصلت إليه (5 أردب قمح) دون اللجوء إلى تخفيض عدد العمال الثمانية هي استعادة النسبة المثلي (4: 1) بين عنصري الإنتاج وذلك عن طريق الانتاج وذلك عن طريق زيادة مساحة الأرض بمقدار فدان آخر. أي تصبح المساحة الإجمالية للأرض التي يعمل عليها العمال الثمانية فدانين اثنين، وبذلك تصبح نسبة العمل إلى الأرض (8: 2) أي (4: 1) وهي النسبة التي تتفق مع تحقيق الحد الأقصى للناتج المتوسط.
و تناقص الغلة هو في الواقع أحد وجهين لحقيقة اقتصادية واحدة، وجهها الآخر يسمي “تزايد التكلفة“. هذه الحقيقة هي أن تناقص الغلة يظهر نتيجة لأن بعض الموارد أكثر ندره من البعض الآخر. وهذا يجعلنا في أحيان كثيرة غير قادرين على زيادة كميات العناصر الأكثر ندره لكي نحتفظ بتلك النسبة بين عوامل الانتاج التي تمكننا من الاستمرار في زيادة كمية الناتج المتوسط. وكما أوضحنا سابقاً، تعني تناقص الغلة أن كل وحدة إضافية من عنصر الانتاج المتغير تأتي بناتج أقل من ناتج الوحدة الواحدة السابقة لها. وواضح أن هذا يعني أيضاً أن الوحدة الواحدة المنتجة تتكلف نفقات متزايدة في شكل استخدام قدر أكبر من عنصر الإنتاج.
مقالة ذات صلة: قانون تناقص الغلة: ما هو، اهميته، مراحله، أمثلة عليه
2. دالة الإنتاج في الأجل الطويل (قوانين الغلة بالنسبة للحجم)
الفترة الطويلة الأجل هي الفترة التي تسمح للمشروع بتغيير الكميات المستخدمة من كافة عناصر الإنتاج الثابتة والمتغيرة. فعندما يتغير بالفعل ما لدي المشروع من عناصر ثابتة للإنتاج مثل المباني والآلات والتجهيزات الأخرى، ويتغير معها ما يتم استخدامه من عناصر انتاجية متغيرة، فإننا نقول إن حجم المشروع قد تغير.
وعند تحليلنا لدالة الإنتاج في الأجل الطويل سنعرض ثبات نسب مزج عناصر الإنتاج بمعنى أن كل عنصر يزداد بنفس النسبة التي تزداد بها العناصر الأخرى. ومعادلة دالة الانتاج كما سبق بيانها: ن ك = د (ل، ض، ر، ت). فإذا افترضنا أن جميع عناصر الإنتاج زادت بنسبة معينة ولتكن 10%، فما أثر ذلك على حجم الناتج الكلي؟. هناك ثلاث حالات محتملة الحدوث في الفترة الطويلة الأجل:
- أن الناتج الكلي يزيد بنسبة أكبر من النسبة التي تزيد بها عناصر الإنتاج. وتسمى هذه بحالة “تزايد غلة الحجم” فإذا زادت عناصر الانتاج بنسبة (10%) فإن الناتج الكلي يزيد مثلاً بنسبة (15%).
- أن الناتج الكلي يزيد بنفي نسبة زيادة عناصر الانتاج. فإذا زادت عناصر الانتاج بنسبة 10% يزيد الناتج بنفس النسبة. ويقال في هذه الحالة أن ظروف الانتاج تخضع لقانون “ثبات غلة الحجم”.
- أن الناتج الكلي يزيد بنسبة أقل من زيادة عناصر الإنتاج. ويقال في هذه الحالة أن ظروف الإنتاج تخضع لقانون “تناقص غلة الحجم”. فإذا زادت عناصر الانتاج بنسبة 10%، فإن الناتج الكلي يزيد بنسبة 8% مثلاً.
وقد فسر بعض الاقتصاديين قانون تزايد الغلة بالنسبة للحجم بكفاءة الآلات والمعدات الكبيرة والتي تكون غير قابلة للانقسام. أما البعض الآخر فيعتقد أن تزايد الغلة مع كبر الحجم (حجم المشروع) تنتج عن إمكانية التخصص وتقسيم العمل أفضل مما يتم في الوحدات الصغيرة. أما تناقص الغلة بالنسبة للحجم فيعتقد أنه نتيجة لكبر حجم الوحدة الانتاجية يصعب إدارتها بطريقة كفء، وينقطع الاتصال الشخصي بين العمال والإدارة، ولا يكون هناك حماس لرفع الانتاجية بذات الدرجة التي تكون قائمة في الوحدات الأصغر من ذلك حجماً.
مقالة ذات صلة: تكلفة الفرصة البديلة: ما هي، أهميتها، عواملها، كيفية حسابها، مثال عليها
فى النهاية آخر نقطة انت من ستضيفها فى التعليقات، شارك غيرك ولا تقرأ وترحل.