القيمة الزمنية للنقود – القيمة الحالية والقيمة المستقبلية
عادة ما تواجه منشأت الأعمال بالعديد من المواقف الاستثمارية التى يمكن من خلالها تحقيق معدلات عائد ايجابية على الاموال المتاحة لديها سواء من خلال الاستثمار فى المشروعات ذات عائد اقتصادى مرتفع او من خلال تحقيق معدلات عائد ايجابية على استثماراتها فى الاوراق المالية سواء فى شكل اسهم او سندات ام من خلال استثمار هذه الاموال فى شكل ودائع بنكية لمدد محددة او استغلال هذه الاموال فى سداد بعض الديون المستحقة على الشركة وبالتالى خفض نسبة المديونية فى هيكلها المالى فضلا عن خفض مدفوعات الفوائد على هذه الديون، بناءاُ على ذلك فان توقيت التدفقات النقدية سواء كانت تدفقات نقدية داخلة او تدفقات نقدية خارجة لها العديد من النتائج الاقتصادية المهمة او التى يجب ان يتفهمها المدير المالى كنتيجة للقيمة الزمنية للنقود٠
إن القيمة الزمنية للنقود تقوم على الحقيقة الثابتة بأن قيمة الجنيه الذى يتم الحصول عليه الان نزيد عن قيمة الجنيه الذى يتم الحصول عليه فى المستقبل نتيجة للتضخم الذى يوجد فى الاتتصاد فكلما زاد معدل التضخم فى الاقتصاد كلما قلت القيمة المستقبلية للنقود عن القيمة الحالية لها
القيمة المستقبلية (Future Value) مقابل القيمة الحالية (Present Value):
الفرق بين القيمة المستقبلية والقيمة الحالية للنقود :-
يمكن اتخاذ القرارات المالية بناءأ على ايجاد قيمة التدفقات النقدية عند نفس النقطة الزمنية سواء باستخدام مفهوم القيمة المستقبلية او باستخدام القيمة الحالية بحيث يكون القرار المالى المناسب هو القرار الذى يحقق اكبر قيمة مستقبلية او اكبرقيمة حالية من بين البدائل المتاحة.
وتعد القيمة المستقبلية والقيمة الحالية وجهى عملة واحدة تعتمد علي القيمة الزمنية للنقود (Time Value of Money). وبالرغم من ان استخدام القيمة المستقبلية او القيمة الحالية سوف يؤدى الى اتخاذ نفس القرار لاختيار البديل الاستثماري أو التمويلي المناسب الا ان طرق حساب القيمة المستقبلية تختلف عن طرق حساب القيمة الحالية.
ان حساب القيمة المستقبلية يعتمد على ايجاد القيمة المتراكمة (Compounding Process) فى نهاية مدة زمنية محددة باستخدام معدل فائدة محددة لمبلغ محدد من المال يتم دفعه مرة واحدة فى بداية المدة (Single Amount) او يتم دفعة خلال الفترة الزمنية على دفعات متساوية (Annuity) او دفعات غير متساوية (Mixed Stream of Cash Flow) ويلاحظ ان عند حساب القيمة المستقبلية فإنه يتم استخدام معدلات الفائدة المركبة (Compound Interest Rate) وليس معدلات الفائدة البسيطة (Simple Interest Rate) ، بمعنى انه يتم الحصول على فائدة على اصل المبلغ بالاضافة الى فائدة على الفائدة التى تحققت فى نهاية كل مدة٠
اما فى حالة حساب القيمة الحالية فانه يتم خصم (Discounting Process) كل التدفقات النقدية خلال فترة مستقبلية سواء كانت هذه التدفقات فى شكل دفعة واحدة سوف يتم الحصول علبها فى نهاية المدة او على شكل دفعات متساوية او غير متساوية يتم الحصول عليها المدى الزمنى وذلك باستخدام معدل فائدة محدد وهو ما يعرف بمعدل الخصم او ما يعرف رأس المال وذلك وصولا الى تحديد قيمة هذه التدفقات النقدية المستقبلية الآن فى الوقت الحاضر (وهو ما بعرف بالوقت صفر).
عند حساب القيمة الحالية أو القيمة المستقبلية للنقود أو التدفقات النقدية، فانه يفضل استخدام الخط الزمنى (Time Line) لتتبع التدفقات النقدية المترتبة على قرار استثماري أو تمويلي معين. والخط الزمنى عباره عن مدى زمنى يوضح عليه الفترات الزمنية بحيث يظهر الوقت فوق الخط بينما يظهر التدفق النقدى (CF) أسفل الخط كما هو موضح فى الشكل القادم (شكل الخط الزمنى).
 |
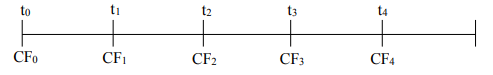| التدفقات النقدية فى نهاية كل سنه |
ان الخط الزمنى يغطى 5 فترات متنالية ( فى هذه الحالة 5 سنوات) كما هو موضح فى الشكل السابق . ان التدفق النقدى فى خلال الزمن صفر وعند نهاية كل سنه موضح تحت الخط الزمنى ويجب ملاحظة ان القيم السالبة توضح التدفقات النقدية الخارجة والقيم الموجبة توضح التدفقات النقدية الداخلة. ان الخط الزمنى يسمح للمحلل المالى بالتفهم الكامل لطبيعة التدفقات النقدية المرتبطة بالاستثمار محل التقييم. وتعبر t0 عن التدفق النقدي في بداية السنة الأولي بينما نعبر t1 عن التدفق النقدي في نهاية السنة الأولي وهي تساوي التدفق النقدي في بداية السنة الثانية …….. وهكذا.
نظرا لان النقود لها قيمة زمنية فان كل التدفقات النقدية المرتبطة بالاستثمار محل التقييم كما هو موضح بالشكل السابق يجب تقييمها عند نفس النقطة الزمنية. وعادة ما يتم تقييم الاستثمارات سواء فى نهاية مدة الاستثمار عن طريق حساب القيمة المستقبلية باستخدام القيمة التراكمية لاصول الاموال التى تم الحصول عليها (او الاموال التى تم ايداعها) فى نهاية فترة الاستثمار بالاضافة الى الفوائد المحققة على الفوائد التى تم تحقيقها من وراء هذه الاموال فى الفترات الزمنية ما قبل نهاية مدة الاستثمار او يتم تحديد القيمة الحالية الان لكل التدفقات النقدية الداخلة خلال الفترات المستقبلية حتى نهاية فترة الاستثمار وذلك عن طريق خصمها باستخدام معدل الخصم المتفق عليه او باستخدام معدل الفائدة السائد فى السوق او باستخدام متوسط التكلفة المرجحة لرأس المال.
و يوضح الشكل القادم القيمة المستقبلية لكل تدفق نقدي عند نهاية فترة الاستثمار والتى تعادل خمس سنوات بإستخدام معدل الاستثمار المناسب، كما يوضح الشكل نفس الشكل القادم القيمة الحالية للتدفقات النقدية الداخلة باستخدام معدل الخصم المناسب لايجاد القيمة الحالية لكل تدفق نقدى عند الوقت صفر بعد ذلك يتم جمع القيم الحالية للتدفقات النقدية لايجاد اجمالى القيمة الحالية للتدفقات النقدية الان. ان معنى وكيفية حساب كل من القيمة الحالية والقيمة المستقبلية للنقود سوف يتم تغطيتها بالتفصيل من خلال هذا الفصل.
 |
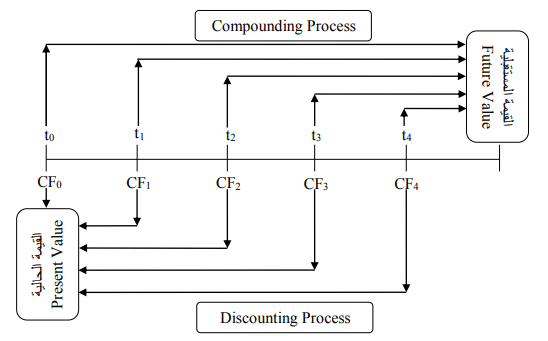| إيجاد القيمة المستقبلية والقيمة الحالية |
وهنا تجدر الاشارة الى انه بالرغم من ان القيمة المستقبلية والقيمة الحالية يعدا وجهى عملة واحدة عند اتخاذ القرارات المالية الا ان المديرين الماليين عادة ما يجب ان يتحذوا قراراتهم الاستثمارية فى ظل القيمة الحالية وليس القيمة المستقبلية لان القيمة الحالية تحت سيطرة المدير المالى بالكامل.
حيث ان التدفقات النقدية المتوقعة سوف تكون واحدة فى ظل حساب القيمة الحالية والقيمة المستقبلية وايضا المدى الزمنى لهذه التدفقات النقدية وكنلك معدل الخصم أو العائد الذى سوف يتم استخدامه لحساب القيمة الحالية او القيمة المستقبلية الا ان المدير المالى يكون مسيطرا تماما على الوضع الحالى بينما الوضع المستقبلى قد يتغير بتغير الحالة الاقصادية للدولة او بتغيير ظروف المنافسة فى السوق مما يؤدى الى اختلاف الواقع عما هو متوقع سواء كان بالنسبة للتدفقات النقدية او بالنسبة لمعدل الخصم أو العائد المستخدم.
مفهوم القيمة المستقبلية
عندما نتحدث عن القيمة المستقبلية فإننا نتحدث عن القيمة التى يتم حسابها باستخدام معدل الفائدة المركب، وليس باستخدام معدل فائدة بسيط. بمعنى ان القيمة المستقبلية لاصل المبلغ فى نهاية المدة سوف يتم حسابه عن طريق حساب الفائدة على اصل المبلغ بالاضافة الى الفائدة على الفوائد (الفائدة على فوائد المبلغ) خلال المدة من تاريخ الايداع وحتى نهاية المدة.
وعندما نتحدث عن اصل المبلغ فان اصل المبلغ يشير الى المبلغ الذى يتم دفع الفائدة عليه بصفة سنوية او نصف سنوية لو ربع سنوية او بمعنى اشمل بصفة دورية. فعادة ما تواجه شركات الاعمال بالعديد من المواقف التى يزيد فيها حجم التدفق النقدى الداخل عن حجم التدفق النقدى الخارج مما يؤدى الى وجود فائض نقدى مع وجود العديد من الفرص لاستغلال هذا الفائض فى تمويل اعمال الشركة او سداد المستحقات عليها لدى الدائنون او استثمار هذا الفائض بطريقة او بأخرى لتعظيم العائد على الاستثمار.
لذا تقوم الشركات بالمفاضلة بين البدائل الاستثمارية المختلفة لاختبار البديل الذى يعظم قيمة المنشأة فى السوق وذلك من خلال حساب القيم المستقبلية للبدائل المختلفة.
القيمة المستقبلية لميلغ واحد (Single Amount) باستخدام المعادلات:
يعد حساب القيمة المستقبلية لمبلغ واحد من أبسط تطبيقات القيمة الزمنية للنقود ويعتمد حساب القيمة المستقبلية علي:
-أصل المبلغ
-مدة الاستثمار
– معدل الفائدة وإذا ما كان سوف يتم دفعه بصفة سنوية، نصف أو ربع سنوية، شهرية.
مثال (1):
بفرض ان شركة أسود البيزنس لديها فائض نقدى يقدر ب 10000 جنيه وليس لدى الشركة اى مجال لاستثمار هذا الفائض غير ايداعه فى حساب استثمارى بالبنك بمعدل فائدة 10 % سنويا.
بنهاية السنة الاولى فان قيمة المبلغ سوف تصبح 11000 جنيه، 10000 جنيه اصل المبلغ بالاضافة إلي فوائد = 10000 × 10 % = 1000 جنيه ويمكن حساب القيمة المستقبلية فى نهاية السنة الاولى باستخدام المعادلة كما يلى:
…………1 (FV1 = PV0 * (1+IR
FV1 = 10,000 * (1 + 10%) 1 = 10,000 * 1.1 = 11,000 LE
FV1 ترمز إلي القيمة المستقبلة فى نهاية السنة الاولى.
PV1 ترمز إلي قيمة النقود فى بداية السنة الاولى.
IR ترمز إلي معدل الفائدة.
وبفرض ان الشركة قد وجدت فى نهاية العام الاول انها ليست في حاجة الى هذا المبلغ لمدة سنة اخرى فقررت استثماره بنفس الشروط لسنة أخري فى هذه الحالة فان الشركة سوف تحصل على فائدة عن ال 10000 جنيه اصل المبلغ بالاضافة الى فائدة علي الفوائد التي بلغت 1000 جنيه بنهاية السنة الأولي ففى نهاية السنة الثانية سوف تحصل الشركة على المبلغ اجمالى قدره 121000 جنيه. ويمكن حساب القيمة المستقبلية فى نهاية السنة الثانية كما يلى:
1 (FV2 = PV1 * (1+IR
FV2= 11,000 * (1 + 10%) 1 = 11,000 * 1.1 = 12,100 LE
أو
2 (FV1 = PV0 * (1+IR
FV2= 10,000 * (1 + 10%) 2 = 10,000 * 1.21 = 12,100 LE
وبفرض ان الموقف قد تكرر للسنة الثالثة فان القيمةالمستقبلية فى نهايةالسنةالثالثةتصبح 13310 جنيه وقد تم حسابها باستخدام المعادلة كما يلى:
1 (FV3 = PV2 * (1+IR
FV3= 12,100 * (1 + 10%) 1 = 12,100 * 1.1 = 13,310 LE
أو
3 (FV3 = PV0 * (1+IR
FV3= 10,000 * (1 + 10%) 3 = 10,000 * 1.331 = 13,310 LE
وعلى ذلك فان المعادلات السابقة تقودنا الى المعادلة العامة لحساب القيمة المستقبلية لمبلغ معين (دفعة واحدة) يتم الحصول عليه فى نهاية مدة زمنية محددة (N) وبمعدل فائدة مركب (IR) على النحو التالى:
N (FVN = PV0 * (1+IR
FVN ترمز إلي القيمة المستقبلة فى نهاية المدة (N).
PV0 ترمز إلي قيمة النقود فى بداية المدة (N).
IR ترمز إلي معدل الفائدة.
N ترمز إلي عدد الفترات.
وبعد ان القينا الضوء على القيمة المستقبلية فى هذة المقالة تبقى ان نتعرف على أمثلة أكثر وان نفهم أكثر كيفية حساب القيمة المستقبلية على دفعات متساوية عادية و دفعات مُقدمة . وان نتعرف على امثلة حياتية بخصوص القيمة المستقبلية. ولذلك تناولنا فى مقالة منفصلة بعنوان القيمة المستقبلية للنقود مع الأمثلة لدفعة واحدة ودفعات متساوية ومُقدمة
مفهوم القيمة الحالية ( Present Value ):
من المفيد عند اتخاذ القرارات التمويلية أو الأستثمارية تحديد قيمة الأموال في الوقت الحالي لكل التدفقات النقدية المستقبلية. وعند حساب القيمة الحالية فإنه يتم خصم التدفقات النقدية المستقبلية المتوقعة باستخدام معدل الخصم المناسب حسب طبيعة المشروع الذي يتم تقييم عوائده. قد يكون هذا المعدل هو سعر الفائدة السائد في السوق أو معدل الفائدة المطلوب عند تقييم البدائل الاستثمارية في شكل اسهم وسندات أو قد يكون تكلفة رأس المال عند تقييم مشروع استثماري.
إيجاد القيمة الحالية لدفعة واحدة يتم الحصول عليها بعد فترة زمنية (N ) بالمعادلات:يعد حساب القيمة الحالية لدفعة واحدة (Present Value of a Single Amount) مشابه لطريقة حساب القيمة المستقبلية لدفعة واحدة. ويعتمد حساب القيمة الحالية علي:
– أصل المبلغ الذي سوف يتم الحصول علية بعد مدة محددة.
– المدة التي في نهايتها سوف يتم الحصول علي المبلغ .
– معدل الخصم.
مثال :
ماهي القيمة الحالية لمبلغ 250000 جنيه من المتوقع الحصول عليه بعد سنة إذا كان معدل الخصم يبلغ 8 % سنويا ؟
يمكن حساب القيمة الحالية باستخدام المعادلة كما يلى:
وبعد ان القينا الضوء على القيمة الحالية فى هذة المقالة تبقى ان نتعرف على أمثلة أكثر وان نفهم أكثر كيفية حساب القيمة الحالية على دفعات متساوية عادية و دفعات مُقدمة . وان نتعرف على امثلة حياتية بخصوص القيمة الحالية . ولذلك تناولنا فى مقالة منفصلة بعنوان القيمة الحالية للنقود مع الأمثلة لدفعة واحدة ودفعات متساوية ومُقدمة
جداول القيمة الزمنية للنقود
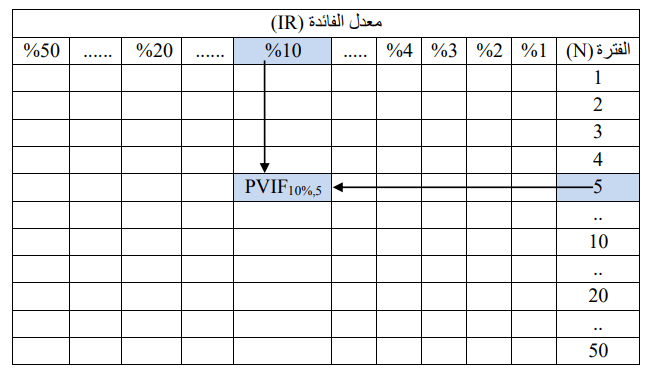
ان ايجاد القيمة المستقبلية او الحالية لدفعة واحدة باستخدام المعادلات التى تم تناولها فى المقالة يستهلك الكثير من الوقت خصوصأ اذا كانت الفترات الزمنية التى يتم حساب القيمة المستقبلية او الحالية فى نهايتها كبيرة كأن تكون 25 سنة او 30 سنه. لذا يفضل الإعتماد على الجداول المالية عند حساب القيمة المستقبلية وذلك عن طريق ايجاد معامل القيمة المستقبلية ( “Future Value Interest Factor “FVIFIR,N) لمبلغ قيمته جنيه واحد يتم استثماره لعدد (N) من الفترات وبمعدل فائدة (IR) من جدول معاملات القيمة المستقبلية الخاص بذلك.
وأيضاً الإعتماد على الجداول المالية عند حساب القيمة الحالية وذلك عن طريق ايجاد معامل القيمة الحالية ( “Present Value Interest Factor “PVIFIR,N) لمبلغ قيمته جنيه واحد يتم استثماره لعدد (N) من الفترات وبمعدل فائدة (IR) من جدول معاملات القيمة الحالية الخاص بذلك.
مثال بالتطبيق على القيمة المستقبلية :
يتم إيجاد التقاطع بين معدل الفائدة (IR) وعدد الفترات (N). وبالتالى يمكن اعادة كتابة المعادلة على النحو التالى.
FVN = PVN * FVIFIR,N
عن طريق هذه المعادلة يمكن ايجاد القيمة المستقبلية فى نهاية الفترة (N) للقيمة الحالية (PV) بإستخدام معدل الفائدة (IR)
كما يمكن حل المثال (1) الذى تناولناه فى بداية هذة المقالة باستخدام جدول القيم المستقبلية (دفعة واحدة) على النحو التالى:
وللتذكير كان نص المثال
بفرض ان شركة أسود البيزنس لديها فائض نقدى يقدر ب 10000 جنيه وليس لدى الشركة اى مجال لاستثمار هذا الفائض غير ايداعه فى حساب استثمارى بالبنك بمعدل فائدة 10 % سنويا.
بنهاية السنة الاولى فان قيمة المبلغ سوف تصبح 11000 جنيه، 10000 جنيه اصل المبلغ بالاضافة إلي فوائد = 10000 × 10 % = 1000 جنيه ويمكن حساب القيمة المستقبلية فى نهاية السنة الاولى بإستخدام الجداول المالية
FV1 = PV0 * FVIF10%,1 = 10,000 * 1.1 = 11,000 LE
FV2 = PV0 * FVIF10%,2 = 10,000 * 1.21 = 12,100 LE
FV3 = PV0 * FVIF10%,3 = 10,000 * 1.331 = 13,310 LE
مثال على القيمة الحالية للنقود
ما هو اقصي مبلغ يمكنك أن تقترضه الآن لمدة ثلاث سنوات بضمان شهادات إدخار قيمتها الأسمية 25000 جنيه وتستحق السداد بعد 3 سنوات من الآن إذا كان معدل الفائدة علي القرض يبلغ %15؟
يمكن حساب القيمة الحالية (PV0 ) باستخدام جداول القيمة الحالية لدفعة واحدة كما يلى:
PV0 = FVN * PVIFIR,N
PV0 = 25,000 * PVIF15%,3 = 25,000 * 0.6575 = 16,437.5 LE
وللعلم : تسطيع بهذة الطريقة حل معادلات القيمة الحالية ومعادلات الدفعات المتساوية والمقدمة للقيمة الحالية والمستقبلية بإستخدام جداول القيمة الزمنية للنقود
تحميل ملف جداول القيمة الزمنية للنقود – جوجل درايف
هدية موقع أسود البيزنس
من الممكن ان تقوم بتحميل ملف أكسيل نوفره لك يقوم بعملية حساب كل عمليات القيمة المستقبلية والحالية ، فكل ما عليك هو إدخال القيم وستظهر النتيجة امامك
تحميل ملف اكسيل لحساب كل عمليات القيمة الزمنية للنقود من جوجل درايف
ملحوظة : الملف باللغة الإنجليزية ولم أقم بترجمته لأن الكلام المستخدمة كلها أساسية لأى شخص يتعامل فى الإدارة المالية مثل
Interest ، Future Value ، Present Value
ولكن لو واجهت صعوبة ممكن ان تقوم بالترجمة من اى مترجم مثل ترجمة جوجل ، واى رموز لا تفهما سوف تجدها مشروحة هنا فى هذة المقالات.
فى النهاية اخر نقطة انت من ستضيفها فى التعليقات، شارك غيرك ولا تقرأ وترحل.
شكرا